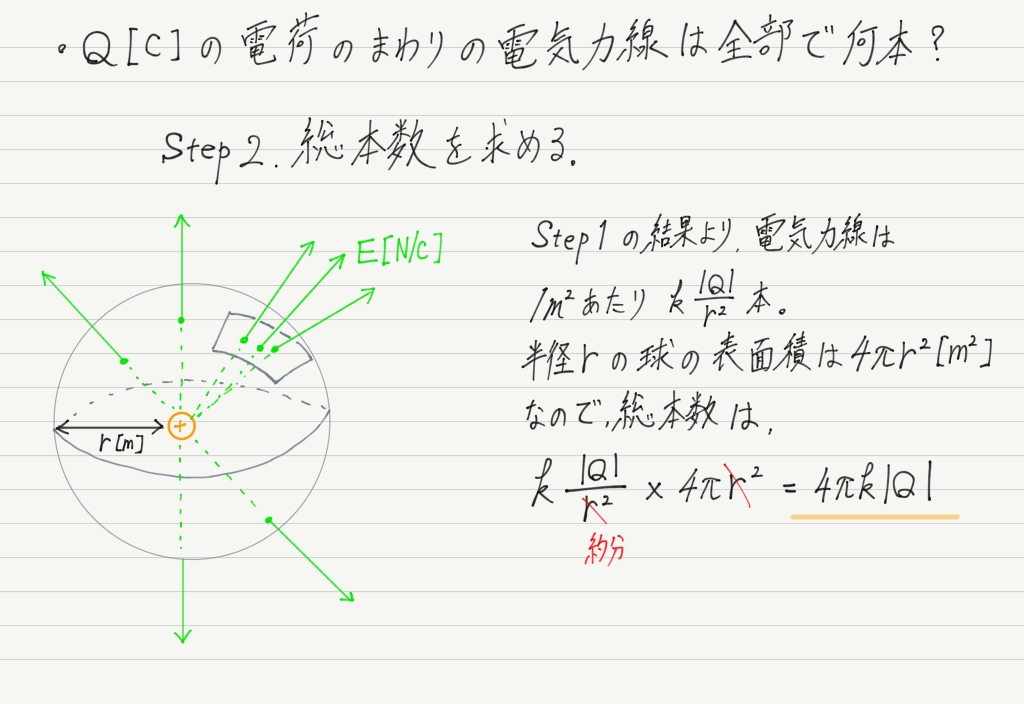
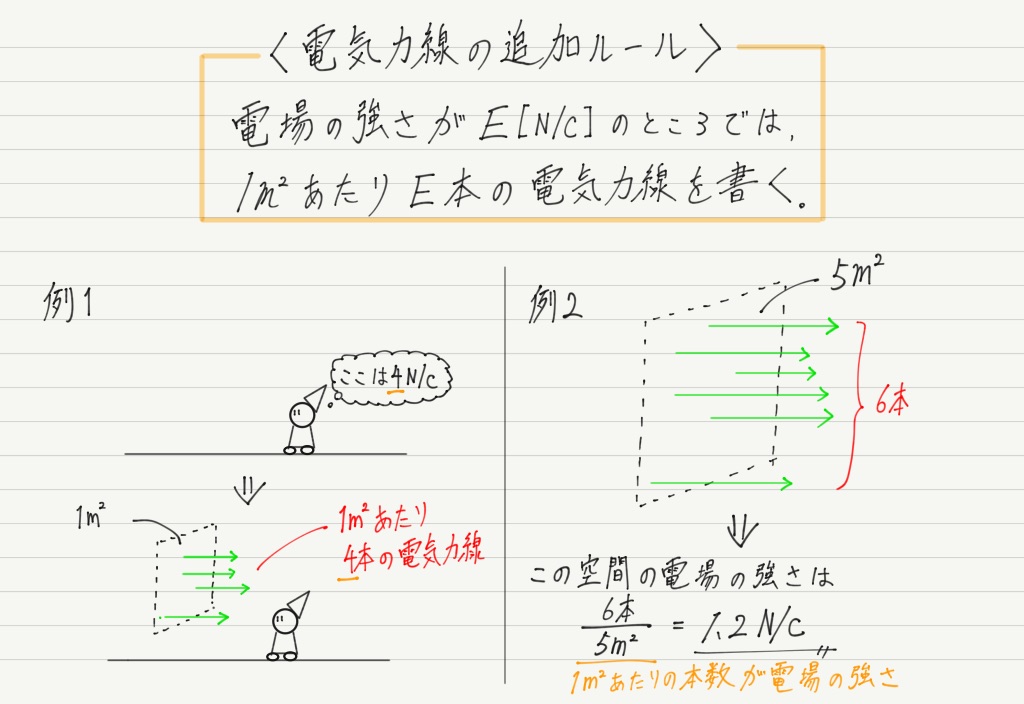
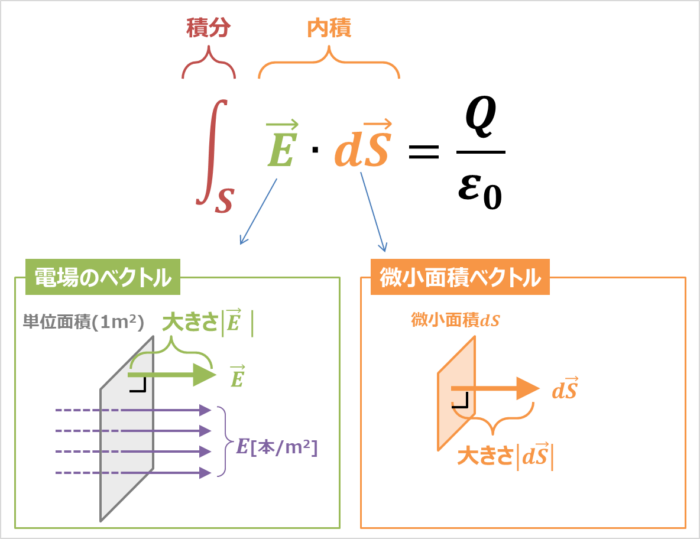
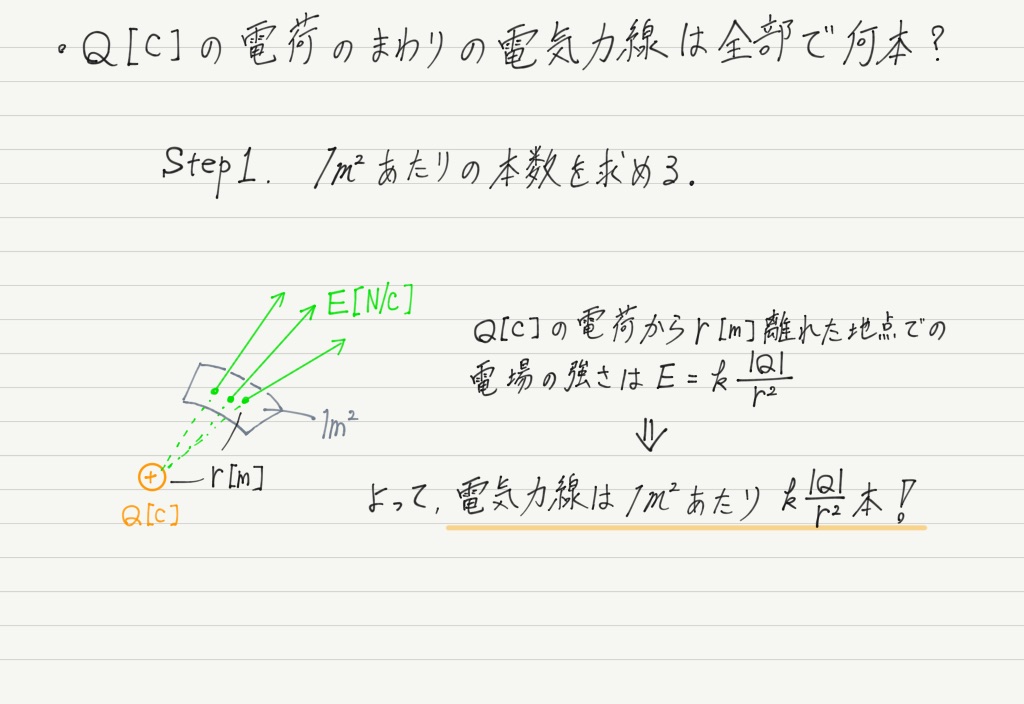
ガウスの法則 自体は、閉曲面内部に存在する 電荷 が形成する 電場 について記述するものですが、閉曲面を貫く 電気力線 の本数についての法則と考えた方が理解し易く、イメージも簡単になります。 さて、 電気力線 に関する ガウスの法則 は次のように述べられます。 電気力線についてのガウスの法則. 閉曲面内部の 電気量 を $Q$ とする。 このとき、閉曲面を貫く 電気力線 の総数 $N$ は次のように与えられる。 \begin {split} N=\int_S\B {E}\cdot\B {n}\,\diff S=4\pi k Q. \end {split} ただし、$k$ を クーロン定数 $\B {E}$ を 電場 、$\B {n}$ を閉曲面の外側を向く法線ベクトルとする。. 磁場に関するガウスの法則. 現在の物理学では電気 (力)と磁気 (力)の間には互いに密接な関係があることがわかっている.しかし, それ以前は電気と似て非なる存在として 磁気 が知られていた. 高校物理では磁気についても議論することになるが, 磁気.

ガウスの法則 高校物理をあきらめる前に読むブログ

ガウスの法則とは？[例題付き] 大学の知識で学ぶ電気電子工学

【高校物理電磁気】ガウスの法則と電場からコンデンサーを考える YouTube

ガウスの法則高校物理をあきらめる前に｜高校物理をあきらめる前に

【ゆっくり解説】ガウスの法則をアニメーション付きで解説【電磁気学】 YouTube

ガウスの法則高校物理をあきらめる前に｜高校物理をあきらめる前に

電場と電気力線、ガウスの法則が分かる!高校物理電磁気

電場の理解が深まる「ガウスの法則」を高校生にもわかるように丁寧に解説！ 黒猫の高校物理

【高校物理】＜コンデンサー②＞電気容量の式をガウスの法則で説明。 YouTube

ガウスの法則が成り立つ理由を説明 Physicmath（フィジクマス）

【高校物理】電気力線の本数4πkq [本]は覚えよう！円柱型ガウスの法則問題＜電磁気第15問＞ YouTube

大学物理 高校物理 ガウスの法則 で 極板間電場を導き Q=CVを導く YouTube

ガウスの法則を徹底解説！【高校物理】 YouTube

【ハイレベル高校物理】クーロンの法則とガウスの法則で電場の求め方を比較 YouTube

電場の理解が深まる「ガウスの法則」を高校生にもわかるように丁寧に解説！ 黒猫の高校物理

【電磁気学】ガウスの法則(平面状に分布している電荷) YouTube

ガウスの法則高校物理をあきらめる前に｜高校物理をあきらめる前に

ガウスの法則を解説！ YouTube

【ガウスの法則とは】『公式』や『積分形』や『微分形』などを解説！

ガウスの法則高校物理をあきらめる前に｜高校物理をあきらめる前に

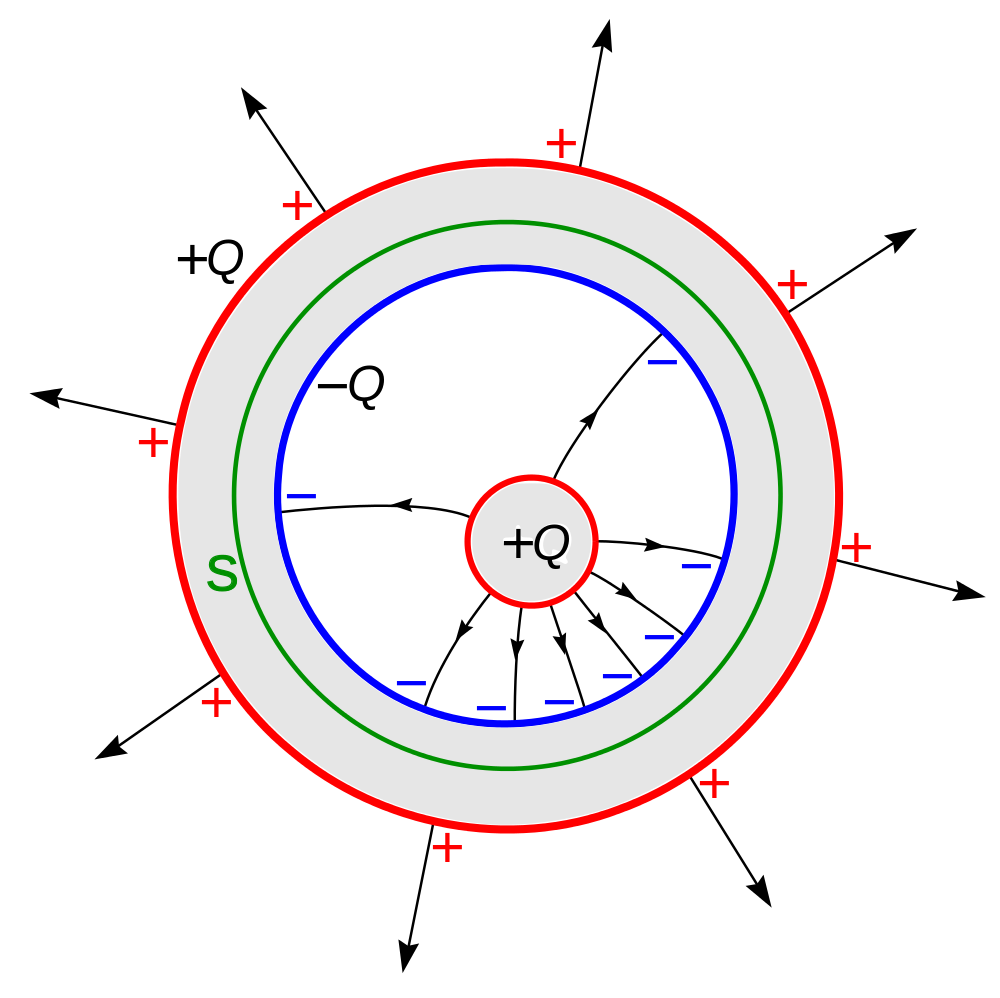
ガウスの法則. 始点と終点がある線分をある領域が取り囲むとき、領域の境界での線分の出入りの総計をカウントすると領域内部の始点と終点の総和が予想できます。 このことを ガウスの定理 といいます。 物理の分野では特に ガウスの法則 といいます。 分かりにくいと思うのでもう一度言い直します。 + の端点から始まって - の端点で終わる線分がいくつかあって、端点をある閉曲面が囲むとき、閉曲面（境界面）を貫く線分を数えると、閉曲面内に存在する端点の総和が分かる、ということです。 線分は途中で途切れたり枝分かれしないものとします。 このとき、出ていく線分は +1本とカウントし、入っていく線分は -1本とカウントします。 左図では、閉曲面内の端点は + が1個と - が1個で総計 0 個です。. 電場の理解が深まる「ガウスの法則」を高校生にもわかるように丁寧に解説! 3枚の極板を並べて作られるコンデンサーにおいて極板を移動させる問題を丁寧に解説!